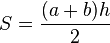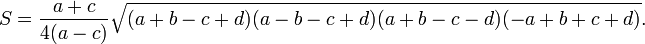Центральный угол

Определение: Центральным углом в окружности называется плоский угол с вершиной в ее центре

• Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу.
• Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Определение: Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.

• Вписанный в окружность угол, стороны которого проходят через две данные точки окружности, равен половине угла между радиусами, проведенными в эти точки, или дополняет эту половину до 180⁰
• Все вписанные в окружность углы. стороны которых проходят через две данные точки окружности, а вершины лежат по одну сторону от прямой, соединяющей эти точки, равны.
• Вписанные углы, стороны которых проходят через концы диаметра окружности, прямые.

Хорда

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности. Часть плоскости, ограниченная окружностью называется кругом. Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Определение: Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны. В окружности равные хорды равноудалены от центра окружности.

Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Сектор

Описанная и вписанная окружность

Определение. Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.

• Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Определение. Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника  и касается всех прямых, проходящих через его стороны.

• Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности. Сам многоугольник в таком случае называется описанным около данной окружности. Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
• Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треугольника это всегда возможно.Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
  • Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
    
  • В любой треугольник можно вписать окружность, и только одну.
  • Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: r=pS , где S — площадь треугольника, а  p=2a+b+c — полупериметр треугольника.
    

  Определение. Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.

  Определение. Окружность называется описанной около треугольника, если она проходит через три его вершины.

  • Вокруг любого треугольника можно описать окружность, и только одну.
  • В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
  • Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника: R=4Sabc, где S — площадь теугольника.

  Определение. Окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон, называется вневписанной.
  

  • Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.

  Окружность, вписанная в прямоугольный треугольник

  • Радиус вписанной окружности находят по формулам: r=aba+b+c, и  r=2a+b−c, где a и b катеты прямоугольного треугольника, а c гипотенуза прямоугольного треугольника.

  Окружность, описанная около прямоугольного треугольника

  • Центр описанной окружности совпадает с серединой гипотенузы.
  • Радиус равен половине гипотенузы: R=2c.
  • Радиус равен медиане, проведенной к гипотенузе: R=mc.

  Четырехугольник, описанный около окружности

  • Четырехугольник ABCD можно описать около окружности, если суммы противолежащих сторон равны AB + CD = BC + AD.
  • Если четырехугольник описан около окружности, то суммы противолежащих сторон равны.
  • Площадь: S=pr, где r — радиус вписанной окружности, а p=2a+b+c+d — полупериметр.

  Четырехугольник, вписанный в окружность

  • Четырехугольник можно вписать в окружность, если сумма противолежащих углов равна 180:+++=180.
  • Если четырехугольник вписан в окружность, то суммы противолежащих углов равны 180.
  • Сумма произведений противолежащих сторон четырехугольника ABCD равна произведению диагоналей: ABDC+ADBC=BDAC.
  • Площадь: S=(p−a)(p−b)(p−c)(p−d) , где p=2a+b+c+d — полупериметр четырехугольника.

  Окружность, вписанная в ромб

  • В любой ромб можно вписать окружность.
  • Радиус r вписанной окружности: r=2h, где h — высота ромба или r=4ad1d2, где a — сторона ромба, d₁ и d₂ — диагонали ромба.

Свойства дуг, хорд и углов окружности

• Если хорды равноудалены от центра окружности, то они равны.
• Если хорды равны, то они равноудалены от центра окружности.
• Большая из двух хорд находится ближе к центру окружности.
• Наибольшая хорда является диаметром.
• Если диаметр делит хорду пополам, то он перпендикулярен ей.
• Если диаметр перпендикулярен хорде, то он делит ее пополам .

• Равные дуги стягиваются равными хордами.
• Дуги, заключенные между параллельными хордами, равны.

• Все вписанные углы, опирающиеся на одну и ту же дугу, раны.
• Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.
• Все вписанные углы, опирающиеся на диаметр, прямые.
• Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180.

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу: =2. Длина хорды: l=2rsin2=2rsin. Длина дуги:  l=r, угол в радианах. Длина окружности: L=2r. Площадь круга: S=r2.

Трапеция

Трапе́ция — четырехугольник, у которого ровно одна пара противолежащих сторон параллельна.

• Параллельные стороны называются основаниями трапеции.
• Две другие стороны называются боковыми сторонами.
• Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
• Расстояние между основаниями называется высотой трапеции.

Виды трапеций

• Трапеция, у которой боковые стороны равны, называется равнобокой (или равнобедренной)
• Трапеция, один из углов которой прямой, называется прямоугольной.

Свойства

• Средняя линия трапеции параллельна основаниям и равна их полусумме.
• Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
• У равнобокой трапеции углы при основании равны.
• У равнобокой трапеции диагонали равны.
• Если трапеция равнобокая, то около нее можно описать окружность.
• Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.
• В трапеции середины оснований, точка пересечения диагоналей и продолжения боковых сторон находятся на одной прямой.

Площадь

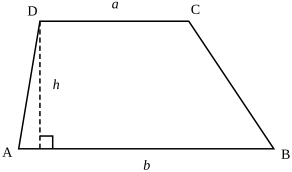
В случае, если a и b — основания и h высота, формула площади:

Формула, где a, b, c и d — стороны трапеции:

Ромб

Определение. Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба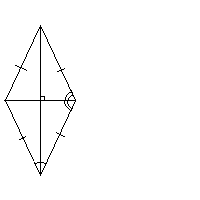

• все свойства параллелограмма:

1. противолежащие стороны равны;
2. противоположные углы равны;
3. диагонали точкой пересечения делятся пополам;
4. сумма углов, прилежащих к одной стороне, равна 180°;
5. сумма квадратов диагоналей равна сумме квадратов всех сторон;

• диагонали перпендикулярны;
• диагонали являются биссектрисами его углов.

Признаки ромба

• Если диагонали параллелограмма перпендикулярны, то параллелограмм — ромб.
• Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм — ромб.

Основные формулы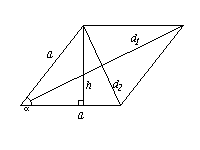

S = ah_a

S = a²sin

S =d₁d₂

Произвольный выпуклый многоугольник

Определение. Объединение замкнутой ломаной и ее внутренней области называют многоугольником.

Саму ломаную называют границей многоугольника, а ее внутреннюю область — внутренней областью многоугольника. Звенья границы многоугольника называются сторонами многоугольника, а вершины — вершинами многоугольника. Отрезок, соединяющий две несоседние вершины многоугольника, называют его диагональю.

Определение. Многоугольник называют выпуклым, если он лежит по одну сторону от каждрй прямой, содержащей его сторону.

Свойства внутренних и внешних угов многоугольника

Теоремы.

• У выпуклого многоугольника каждый угол меньше 180.
• Сумма внутренних углов выпуклого n -угольника равна (n−2)180.
• Сумма внешних углов, взятых по одному у каждой вершины, равна 2.

Правильный многоугольник

Определение. Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.

Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.

Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.

Свойства правильного многоугольника. Правильный многоугольник является вписанным в окружность и описанным около окружности, при этом центры этих окружностей совпадают Центр правильного многоугольника совпадает с центрами вписанной и описанной окружностей. Сторона an правильного n-угольника связана с радиусом R описанной окружности формулой an =2Rsin n180 =2Rsin n . Периметры правильных n-угольников относятся как радиусы описанных окружностей.

Формулы

• Пусть R — радиус описанной вокруг правильного многоугольника окружности, тогда радиус вписанной окружности равен r=Rcosn , а длина стороны многоугольника равна a=2Rsinn .
  
• Площадь правильного многоугольника с числом сторон n и длиной стороны a составляет S=4na2ctgn.
• Площадь правильного многоугольника с числом сторон n, вписанного в окружность радиуса R составляет S=2nR2sinn2.
• Площадь правильного многоугольника с числом сторон n, описанного вокруг окружности радиуса r составляет S=nr2tgn.

Параллелограмм

Определение. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны, т.е. лежат на параллельных прямых.