Правильная пирамида

Определение. Многогранник, у которого одна грань, называемая основанием, – многоугольник, а другие грани – треугольники с общей вершиной, называется пирамидой.

Грани, отличные от основания, называются боковыми. Общая вершина боковых граней называется вершиной пирамиды. Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. Высотой пирамиды H называется перпендикуляр, проведенный из вершины пирамиды на ее основание.

Определение. Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.

Определение. Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.

Определение. Плоскость, параллельная основанию пирамиды, отсекает ее на подобную пирамиду и усеченную пирамиду.

Свойства правильных пирамид

• Боковые ребра правильной пирамиды — равны.
• Боковые грани правильной пирамиды — равные друг другу равнобедренные треугольники.

Особые случаи пирамиды

Если все боковые ребра равны, то

• высота проектируется в центр описанной окружности;
• боковые ребра образуют с плоскостью основания равные углы.

Если боковые грани наклонены к плоскости основания под одним углом, то

• высота проектируется в центр вписанной окружности;
• высоты боковых граней равны;
• площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани

Куб

Куб или гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат, частный случай параллелепипеда и призмы.

Свойства куба

• В куб можно вписать тетраэдр, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба. Все шесть ребер тетраэдра будут лежать на всех шести гранях куба и равны диагонали грани-квадрата.
• Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырем его диагоналям.
• В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
• Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
• В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

вершин 8 площадь поверхности 6a2 ребер 12 радиус вписанной сферы 21a граней 6 радиус описанной сферы 23a граней при вершине 3 угол наклона грани 90 длина ребра a угол наклона ребра 90

Действие над векторами и их свойства

Определение. Вектор — это направленный отрезок.

Определение. Суммой векторов − a(a1 ;a2 ) и − b(b1;b2) называется вектор −ca1+b1;a2+b2 , т.е. −aa1;a2 +−bb1;b2=−ca1+b1;a2+b2 .

Для любых векторов −a(a1;a2) и −b(b1;b2) справедливы равенства:

• переместительный закон: −a+−b=−b+−a;
• сочетательный закон: −a+(−b+−c)=(−a+−b)+−c;
• из переместительного и сочетательного законов следует, что, складывая любое число векторов, можно как угодно переставлять и группировать слагаемые.

Для любых векторов −a(a1;a2), −b(b1;b2) и чисел ,  $$\mu$$ справедливы два распределительных закона:

• (+)−a=−a+−a
• (−a+−b)=−a+−b

Определение. Скалярным произведением двух ненулевых векторов называют произведение длин этих векторов на косинус угла между ними: S=−a−b=−a−bcos, если угол между векторами равен $$\phi$$.

• Если хотя бы один из двух векторов нулевой, то их скалярное произведение равно 0: S=−a−b=0
• Если векторы −a и −b равны, то S=(−a)2 и  говорят о скалярном квадрате вектора.В этом случае cos=1, т.е. S=−a2. Итак, скалярный квадрат вектора совпадает и квадратом его длины: (−a)2 =−a2 .
• Если векторы −a и −b перпендикулярны, то S=−a−b=0. Векторы −a и −b перпендикулярны в том и только в т ом случае, когда их скалярное произведение равно нулю.

Для любых векторов −a, −b, −c и числа справедливы равенства:

• (−a−b)=(−a−b)
• −a(−b+−c)=−a−b +−a−c.

Аналогично рассматриваются вектора и в пространстве.

Скалярное произведение

Рассмотрим два произвольных вектора:  − a(a1 ;a2 ;a3 ) и −b(b1;b2;b3)

Определение. Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.

Определение. Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так: ∠(−a−b) .

Определение. Скалярным произведением векторов −a и −b называется произведение их длин на косинус угла между ними: (−a−b)=−a−bcos∠(−a−b) .

Определение. Скалярным произведением векторов называется произведение их длин на косинус угла между ними:

Утверждения:

• Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
• Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.
• Скалярное произведение двух векторов −a(a1;a2;a3) и −b(b1;b2;b3), заданных своими координатами, может быть вычислено по формуле (−a−b)=a1b1+a2b2+a3b3.

Основные свойства скалярного произведения

Для любых векторов  −a, −b и −c и любого числа справедливы равенства:

• (−a)2=(−a−b)0, причем  (−a)2=0−a=−0;
• переместительный закон: (−a−b)=(−b−a);
• распределительный закон: (−a+−b−c)=(−a−c)+(−b−c);
• сочетательный закон: (−a−b)=(−a−b).

Перпендикулярность векторов

Условие перпендикулярности векторов

• Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
• Даны два вектора  a (xa;ya) и b(xb;yb). Эти векторы будут перпендикулярны, если выражение x_ax_{b +} y_ay_b = 0.

Условие коллиневрности векторов

• Векторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.
• Даны два вектора a(xa;ya) и b(xb;yb). Эти векторы коллинеарны, если x_a = λ x_b и y_a = λ y_b, где R.

Декартовы координаты вектора в пространстве

Прямые x, y, z называются координатными осями (или осями координат), точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.

Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OA_x: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.

Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).

Определение. Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Единичный вектор, направленный вдоль оси x, обозначается i. Единичный вектор, направленный вдоль оси y, обозначается j. Единичный вектор, направленный вдоль оси z, обозначается k. Определение. Вектора i, j, k называются координатными векторами. Эти векторы некомпланарны, а значит, любой вектор a можно разложить по координатным векторам: a=xi+yj+zk. Коэффициенты разложения определяются единственным образом и называются координатами вектора a в данной системе координат.

Свойства векторов, заданных координатами

• Координаты нулевого вектора равны нулю.
• Координаты равных векторов соответственно равны.
• Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.
• Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.
• Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.

Формулы

Угол между векторами: $$\vec a(x_{a};y_{a};z_{a}), \quad \vec b(x_{b};y_{b};z_{b})  \Rightarrow cos\gamma = \frac{x_{a} \cdot x_{b}+ y_{a} \cdot y_{b}+ z_{a} \cdot z_{b}}{\sqrt{x_{a}^{2}+y_{a}^{2}+z_{a}^{2}} \cdot \sqrt{x_{b}^{2}+y_{b}^{2}+z_{b}^{2}}}$$

Перпендикулярность векторов: $$\vec a(x_{a};y_{a};z_{a}), \quad \vec b(x_{b};y_{b};z_{b})  \Rightarrow \vec a \cdot \vec b = 0 \Leftrightarrow
x_{a} \cdot x_{b}+ y_{a} \cdot y_{b}+ z_{a} \cdot z_{b}= 0$$

Коллинеарность векторов: $$\vec a(x_{a};y_{a};z_{a}), \quad \vec b(x_{b};y_{b};z_{b})  \Rightarrow  \frac{x_{a}}{x_{b}}=\frac{y_{a}}{y_{b}}=\frac{z_{a}}{z_{b}}$$ если координаты векторов не равны нулю.

Декартова система координат

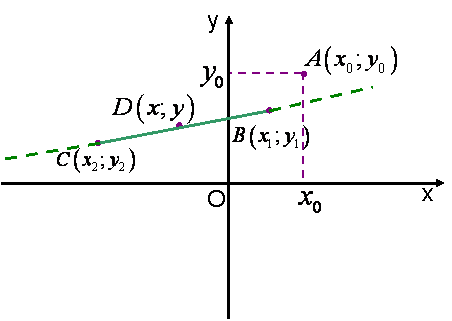
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для обеих осей.

Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° еe положительное направление совпало с положительным направлением оси OY. Четыре угла (I, II, III, IV), образованные осями координат OX и OY, называются координатными углами

Положение точки A на плоскости определяется двумя координатами x₀ и y₀. Координата x₀ называется абсциссой точки A, координата y — ординатой точки A.

Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Расстояние между двумя точками: BC=(x1−x2)2+(y1−y2)2

Координаты середины отрезка BC: x=2x1+x2y=2y1+y2

Координаты точки, делящей отрезок в заданном отношении: если DBCD=k2k1, то x=k2k1+k2x1+k1k1+k2x2,  y=k2k1+k2y1+k1k1+k2y2

Уравнение прямой, проходящей через две заданные точки: (y — y₁)(x₂ — x₁) = (x — x₁)(y₂ — y₁).  Если x1=x2y1=y2 , то это уравнение можно записать в виде  y−y1y2−y1=x−x1x2−x1

Уравнение окружности с центром в начале координат: x² + y² = R²

Уравнение окружности с центром в  точке (x₀;y₀₎ : (x — x₀)² + (y — y₀)² = R²

Прямые и отрезки в окружности

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Расстояние то точки окружности до ее центра называется радиусом окружности. Отрезок, соединяющий любые точки окружности, называется хордой. Хорда, проходящая через центр окружности называется диаметром. Прямая, проходящая через люьые точки окружности, называется секущей.

Углы между прямыми и отрезками окружности

Угол между пересекающимися хордами =2+	Угол между секущими, пересекающимися вне окружности =2−	Угол между касательной и секущей =2−	Угол между касательными =2−=−	Угол между касательной и хордой =2

Соотношения между прямыми и отрезками окружности

Отрезки пересекающихся хорд связаны соотношением: ab=cd	Отрезки касательных, проведенных из одной точки, равны: AB = AC	Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки: AB2=ACAD	Произведения отрезков секущих, проведенных из одной точки, равны: ABAC=ADAE

Углы в окружности. Свойства углов, связанных с окружностью.

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром

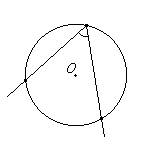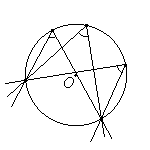
Свойства углов, связанных с окружностью

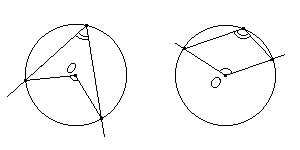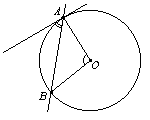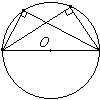
Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.	Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.	Вписанный угол, опирающийся на диаметр, равен 90°.	Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.

Свойства окружности

Свойства окружности

• Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC² = MA•MB.

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.