Правильный тетраэдр с примерами

Правильный тетраэдр - это правильная треугольная пирамида у которой все грани являются равносторонними треугольниками.

У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

У тетраэдра 4 грани, 4 вершины и 6 ребер. 

Основные формулы для правильного тетраэдра приведены в таблице.

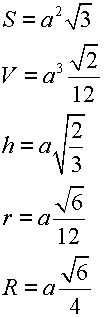
Где:
S — Площадь поверхности правильного тетраэдра
V — объем
h — высота, опущенная на основание
r — радиус вписанной в тетраэдр окружности
R — радиус описанной окружности
a — длина ребра

Практические примеры

Задача.
Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро равно √3 

Решение.
Поскольку все ребра треугольной пирамиды равны — она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a²√3 .
Тогда
S = 3√3

Ответ: 3√3

Задача.
Все ребра правильной треугольной пирамиды равны 4 см. Найдите объем пирамиды

Решение.
Поскольку в правильной треугольной пирамиде высота пирамиды проецируется в центр основания, который одновременно является центром описанной окружности, то

AO = R = √3 / 3 a
AO = 4√3 / 3

Таким образом, высота пирамиды OM может быть найдена из прямоугольного треугольника AOM

AO² + OM² = AM²
OM² = AM² - AO²
OM² =  4² - ( 4√3 / 3 )²
OM² = 16 — 16/3
OM = √(32/3)
OM = 4√2 / √3

Объем пирамиды найдем по формуле V = 1/3 Sh
При этом площадь основания найдем по формуле S = √3/4 a²

V = 1/3 (√3 / 4 * 16 ) ( 4√2 / √3 )
V = 16√2 / 3