Квадрат
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Определение. Прямоугольник, у которого все стороны равны, называется квадратом.
Свойства и признаки квадрата (необходимые и достаточные условия того, что четырехугольник — квадрат)
- Если четырехугольник — квадрат, то для него справедливы все следующие утверждения.
- Если для четырехугольника справедливо хотя бы одно из следующих утверждений, то он — квадрат.
Утверждения.
- Все стороны равны и среди внутренних углов есть прямой угол.
- Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
- Четырехугольник имеет 4 оси симметрии: прямые, перпендикулярные сторонам и проходящие через их середины; прямые, содержащие диагонали.
- Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90
 .
.
 |
 |
Около квадрата можно описать окружность. Радиус описанной окружности выражается через сторону a квадрата и его диагональ d: R=a 2=2d 2=2d |
 |
В квадрат можно вписать окружность. Радиус вписанной окружности равен половине стороны: r=2a |
Выпуклый четырехугольник
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Определение: Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
- Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.
- Вершины, не являющиеся соседними, называются противоположними.
- Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями.
- Стороны четырехугольника, исходящие из одной вершины, называются соседними сторонами.
- Стороны, не имеющие общего конца, называются противолежащими сторонами.
- Четырехугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую его сторону.
 |
Виды четырехугольников
- Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны
- Прямоугольник — параллелограмм, у которого все углы прямые
- Ромб— параллелограмм, у которого все стороны равны
- Квадрат — прямоугольник, у которого все стороны равны
- Трапеция — четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны
- Дельтоид — четырехугольник, у которого две пары смежных сторон равны
Углы на плоскости
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Ключевые слова: угол, плоскость, прямая, смежный угол, вертикальный угол, внутренний односторонний угол
Определение. Углом называется фигура, состоящая из двух лучей с общим началом и ограниченной ими части плоскости.
Точка, из которой выходят ограничивающие угол лучи, называется вершиной угла, а сами лучи — сторонами угла. Слово «угол» иногда заменяют знаком ∠ . Часто при изображении угла чертят только выходящие из вершины начальные участи его сторон, а ту часть, которую хотят указать, обозначают дужкой.
 |
Угол обозначается или одной заглавной буквой, поставленной у вершины угла, например: ∠A , или тремя буквами, из которых одна ставится при вершине угла, а две другие — у каких-нибудь точек сторон, например: ∠BAD . Буква, стоящая при вершине угла, всегда записывается между двумя другими буквами. Иногда угол обозначают цифрой, поставленной внутри угла. |
 |
Острый угол имеет градусную меру меньше чем 900
Прямой угол равен 900 . Тупой угол имеет градусную меру больше чем 900 . Развернутый угол равен 1800. |
Определение. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
Свойства смежных углов.
- Если два угла равны, то смежные с ними углы равны.
- Угол, смежный с прямым углом, есть прямой угол.
- Угол, смежнй с острым, является тупым, а смежный с ним тупой — острым.
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
При пересечении двух параллельных прямых третьей, называемой секущей:
- Секущая обязательно пересекает обе прямые.
- При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Накрест лежащие углы равны.
- Соответственные углы равны.
- Односторонние углы в сумме составляют 180°.
- Смежные углы в сумме составляют 180°, а вертикальные — равны.

Равносторонний треугольник
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
 |
Определение. Треуго́льник — простейший многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.
Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (α,β,γ), а длины противоположных сторон — прописными латинскими буквами (a, b, c). |
Определение. Правильный треугольник или равносторонний треугольник — правильный многоугольник с тремя сторонами. Все стороны равны между собой, и все углы равны 60° (или π / 3).
 |
Пусть t — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
|
Свойства.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
Равнобедренный треугольник
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Определение. Равнобедренный треугольник — треугольник, в котором две стороны равны между собой. По определению, правильный треугольник также является равнобедренным, но обратное, вообще говоря, неверно.
 |
Свойства
Признаки
|
Пусть a — длина двух равных сторон равнобедренного треугольника, b — длина третей стороны, α и β — соответствующие углы, R — радиус описанной окружности, r — радиус вписанной окружности.
Соотношения для сторон:
- a=2R
 sin
sin
 b=2R
b=2R  sin
sin (теорема синусов );
(теорема синусов ); - a=b2cos
 (следствие теоремы косинусов);
(следствие теоремы косинусов); - b=a
 2(1−cos
2(1−cos ) (следствие теоремы косинусов);
) (следствие теоремы косинусов); - b=2a
 cos
cos (теорема о проекциях).
(теорема о проекциях).
Соотношения для углов:
 =2
=2 −
− ;
;
 =
= −2
−2 ;
; =arcsina2R
=arcsina2R
 =arcsinb2R.
=arcsinb2R.
Соотношения для периметра:
- P = 2a + b (по определению);
- P=2R(2sin
 +sin
+sin ).
).
Соотношения для площади:
- S=21a2sin
 =21absin
=21absin ;
; - S=21b
 a2−41b2 (формула Герона).
a2−41b2 (формула Герона).
Прямоугольный треугольник
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Определение. Треугольник называют прямоугольным, если у него есть прямой угол.
- Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
- Сумма двух острых углов прямоугольного треугольника равна прямому углу.
- Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
- Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
- Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности. Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СD = hc из вершины С его прямого угла.
Она разобьет данный треугольник на два прямоугольных треугольника АСD и ВСD; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС.
Все три треугольника АВС, АСD и ВСD подобны между собой.

Из подобия треугольников определяются соотношения:
- h=
 ac
ac bc=ca
bc=ca b ;
b ; - c = ac + bc;
- a=
 ac
ac c
c b=
b= bc
bc c ;
c ; - (ba)2=bcac .
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
Геометрическая формулировка. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Алгебраическая формулировка. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b: a2 + b2 = c2
Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.

Виды треугольников
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Определение. Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Определение. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Определение. Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Определение. Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Определение. Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Определение. Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Решение треугольников
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Решение прямоугольных треугольников
 |
Рассмотрим прямоугольный треугольник ABC. В нем
|
Решение произвольных треугольников
Для решения произвольных треугольников существует теорема косинусов и теорема синусов.
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
- Формула a2=b2+c2−2b
 c
c cos∠A ( или формула b2=a2+c2−2a
cos∠A ( или формула b2=a2+c2−2a c
c cos∠B или формула c2=b2+a2−2b
cos∠B или формула c2=b2+a2−2b a
a cos∠C ) позволяет вычислить длину одной из сторон треугольника по данным длинам двух других сторон и величине угла, лежащей против неизвестной стороны.
cos∠C ) позволяет вычислить длину одной из сторон треугольника по данным длинам двух других сторон и величине угла, лежащей против неизвестной стороны. - Теорема косинусов позволяет также по даннм величинам сторон треугольника вычислить величины его углов: cos∠A=2b
 cb2+c2−a2 ; cos∠B=2a
cb2+c2−a2 ; cos∠B=2a ca2+c2−b2 ; cos∠C=2a
ca2+c2−b2 ; cos∠C=2a ba2+b2−c2 .
ba2+b2−c2 .
Теорема синусов. Стороны треугольника пропорционально синусам противоположных углов asin∠A=bsin∠B=csin∠C , где a, b, c — стороны треугольника.
Теорема синусов позволяет по двум сторонам и углу, лежащему против одной из них (или по стороне и двум углам) вычислить остальные элементы треугольника.

Площадь треугольника
in Конспекты по геометрии
as доказательство, Конспекты по геометрии, лекции, теорема
Обозначения:
- ha - высота, проведенная к стороне a.
- p — полупериметр, т.е. половина от суммы всех сторон треугольника.
- R — радиус описанной окружности.
- r — радиус вписанной окружности.

Средняя линия
in Конспекты по геометрии
as длина отрезка, доказательство, Конспекты по геометрии, лекции, отрезок, средняя линия, средняя линия трапеции, средняя линия треугольника, средняя линия четырехугольника, теорема, треугольник
- Определение. Отрезок, соединяющий середины противолежащих сторон четырехугольника, называется средней линией четырехугольника.
- Теорема. Если в выпуклом четырехугольнике прямая, проходящая через середины двух противоположных сторон, образует равные углы с диагоналями четырехугольника, то диагонали равны.
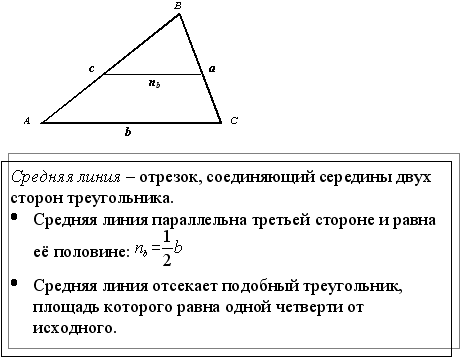
- Определение. Средняя линия треугольника - это отрезок, соединяющий середины двух его сторон.
- Теорема. Средняя линия треугольника параллельна третьей стороне, а ее длина равна половине длины этой стороны.
- Определение. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
- Теорема. Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме длин оснований.
- Теорема. Середины сторон равнобедренной трапеции являются вершинами ромба.